С1-1. Два одинаковых бруска, связанные легкой пружиной, покоятся на гладкой горизонтальной поверхности стола. В момент t = 0 правый брусок начинают двигать так, что за время х он набирает конечную скорость и движется затем равномерно по прямой, совпадающей с осью пружины. За время τ левый брусок успевает сместиться значительно меньше, чем правый. Каков характер движения левого бруска относительно стола при t > τ? Ответ поясните, указав, какие физические явления и закономерности вы при этом использовали.  

С1-2. Деревянный брусок плавает на поверхности воды в миске. Миска покоится на поверхности земли. Что произойдет с глубиной погружения бруска в воду, если миска будет стоять на полу лифта, который движется с ускорением, направленным вертикально вверх? Ответ поясните, указав, какие физические явления и закономерности вы при этом использовали.

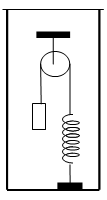С2-3. В сосуде (см. рисунок) находится система тел, состоящая из блока с перекинутой через него легкой нитью, к концам которой привязаны тело объёмом V и пружина жёсткостью k. Нижний конец пружины прикреплён ко дну сосуда. Как изменится сила натяжения нити, действующая на пружину, если эту систему целиком погрузить в жидкость плотностью ρ? (Считать, что трение в оси блока отсутствует.)  

С2-4. Автомобиль совершает поворот на горизонтальной дороге по дуге окружности радиуса 81 м. Какова максимальная скорость автомобиля при коэффициенте трения автомобильных шин о дорогу 0,4? 

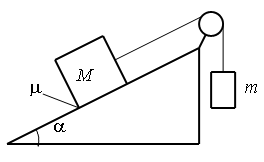С2-5. Грузы массами М = 1 кг и m связаны лёгкой нерастяжимой нитью, переброшенной через блок, по которому нить может скользить без трения (см. рисунок). Груз массой М находится на шероховатой наклонной плоскости (угол наклона плоскости к горизонту α = 30°, коэффициент трения μ = 0,3). Чему равно максимальное значение массы m, при котором система грузов ещё не выходит из первоначального состояния покоя?

С2.6. Брусок массой m₁ = 1 кг лежит на наклонной плоскости с углом при основании, равным α = 53°. Коэффициент трения бруска с плоскостью равен μ = 0,5. К бруску привязана невесомая нить, другой конец которой перекинут через неподвижный идеальный блок. К этому концу нити подвешивается груз массой m₂ = 1 кг. Определите, придет ли в движение брусок при подвешивании груза. Если придет в движение, то в каком направлении? (sin 53° = 0,8; cos 53° = 0,6) 

С2-7. Грузовой автомобиль со всеми ведущими осями массой М = 4 т тянет за нерастяжимый трос вверх по уклону легковой автомобиль массой m = 1 т, у которого выключен двигатель. С каким максимальным ускорением могут двигаться автомобили, если угол уклона составляет α = arcsin 0,1, а коэффициент трения между шинами грузового автомобиля и дорогой μ = 0,2? Силой трения качения, действующей на легковой автомобиль, пренебречь. Массой колес пренебречь.  

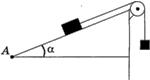С2-8. На наклонной плоскости находится брусок, связанный с грузом перекинутой через блок нерастяжимой нитью (см. рисунок). Угол наклона а плоскости равен 30°, масса бруска — 2 кг, коэффициент трения бруска о плоскость равен 0,23, масса груза — 0,2 кг. В начальный момент времени брусок покоился на расстоянии 5 м от точки А у основания плоскости. Определите расстояние от бруска до точки А через 2 с после начала движения.

С2-9. Система грузов M, m₁ и m₂ показанная на рисунке, движется из состояния покоя. Поверхность стола - горизонтальная гладкая. Коэффициент трения между грузами M и m₁ равен μ = 0,2. Грузы М и m₂ связаны легкой нерастяжимой нитью, которая скользит по блоку без трения. Пусть M = 1.2 кг, m₁ = m₂ = m. При каких значениях m грузы M и m₁ движутся как одно целое?

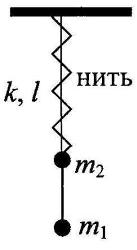С2-10. Материальные точки массами m₁ = 100 г и m₂ = 200 г прикреплены к невесомому стержню, как показано на рисунке. К точке m₂ прикреплена невесомая пружина жесткостью k = 30 Н/м, верхний конец которой закреплен. Длина пружины в недеформированном состоянии l₀ = 20 см. В начальный момент концы пружины связаны нитью длиной l = 10 см. Определите силу реакции стержня, действующую на массу m₂ сразу после пережигания нити.  

С2-11. В аттракционе человек массой 70 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. Каков радиус круговой траектории, если в верхней точке сила давления человека на сидение тележки равна 700 Н при скорости движения тележки 10 м/с? Ускорение свободного падения принять равным 10 м/с².  

С2-12.  В аттракционе человек массой 80 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. Каков радиус круговой траектории, если в верхней точке сила давления человека на сидение тележки равна 200 Н при скорости движения тележки 7,5 м/с? Ускорение свободного падения принять равным 10 м/с².

С2.13.В аттракционе человек массой 80 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. Каков радиус круговой траектории, если при скорости 10 м/с, направленной вертикально вверх, сила нормального давления человека на сидение тележки равна 1600 Н? Ускорение свободного падения равно 10 м/с². 

С2.14. В аттракционе человек массой 60 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. Какова сила давления человека на сидение тележки в нижней точке при движении тележки со скоростью 10 м/с, если радиус круговой траектории 10 м? Ускорение свободного падения принять равным 10 м/с². 

С2-15. В аттракционе человек массой 100 кг совершает «мертвую петлю» в вертикальной плоскости. Когда вектор скорости был направлен вертикально вниз, сила нормального давления человека на сидение была 2000 Н. Найдите скорость тележки в этой точке при радиусе круговой траектории 5 м. Ускорение свободного падения 10 м/с².  

С2.16. В аттракционе человек движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. С какой скоростью должна двигаться тележка в верхней точке круговой траектории радиусом 6,4 м, чтобы в этой точке сила давления человека на сидение тележки была равна 0 Н? Ускорение свободного падения 10 м/с². 

С2.17. В аттракционе человек движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. С какой скоростью должна двигаться тележка в верхней точке круговой траектории радиусом 4,9 м, чтобы в этой точке сила давления человека на сидение тележки была равна 0 Н? Ускорение свободного падения 10 м/с². 

С2.18. В аттракционе человек массой 70 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. С какой скоростью движется тележка в верхней точке круговой траектории радиусом 5 м, если в этой точке сила давления человека на сидение тележки равна 700 Н? Ускорение свободного падения принять равным 10 м/с². 

С2.19. В аттракционе человек массой 70 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. С какой скоростью двигалась тележка в нижней точке круговой траектории радиусом 5 м, если в этой точке сила давления человека на сидение тележки была равна 2100 Н? Ускорение свободного падения 10 м/с². 

С2-20. Шарик скользит без трения по наклонному желобу, а затем движется по «мертвой петле» радиусом R. С какой силой шарик давит на желоб в нижней точке петли, если масса шарика равна 100 г, а высота, с которой его отпускают, равна 4R?

С2-21. Средняя плотность планеты Плюк равна средней плотности Земли, а первая космическая скорость для Плюка в 2 раза больше, чем для Земли. Чему равно отношение периода обращения спутника, движущегося вокруг Плюка по низкой круговой орбите, к периоду обращения аналогичного спутника Земли? Объем шара пропорционален кубу радиуса (V ~ R³).  

С2-22. Радиус планеты Плюк в 2 раза меньше радиуса Земли, а период обращения спутника, движущегося вокруг Плюка по низкой круговой орбите, совпадает с периодом обращения аналогичного спутника Земли. Чему равно отношение средних плотностей Плюка и Земли? Объём шара пропорционален кубу радиуса (V ~ R³).

С2-23. Масса Марса составляет 0,1 массы Земли, диаметр у Марса вдвое меньше, чем у Земли. Каково отношение периодов обращения искусственных спутников Марса и Земли —T_М / T_З, движущихся по круговым орбитам на небольшой высоте?  

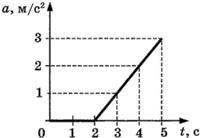С2-24. К покоящемуся на шероховатой горизонтальной поверхности телу приложена нарастающая с течением времени горизонтальная сила тяги F = bt, где b — постоянная величина. На рисунке представлен график зависимости ускорения тела от времени действия силы. Определите коэффициент трения скольжения.  

С2-25. Полый конус с углом при вершине 2α вращается с угловой скоростью ω вокруг вертикальной оси, совпадающей с его осью симметрии. Вершина конуса обращена вверх. На внешней поверхности конуса находится небольшая шайба, коэффициент трения которой о поверхность конуса равен μ. При каком максимальном расстоянии L от вершины шайба будет неподвижна относительно конуса? Сделайте схематический рисунок с указанием сил, действующих на шайбу. 

С2-26. Полый конус с углом при вершине 2α вращается с угловой скоростью ω вокруг вертикальной оси, совпадающей с его осью симметрии. Вершина конуса обращена вверх. На внешней поверхности конуса находится небольшая шайба. При каком минимальном коэффициенте трения шайба будет неподвижна относительно конуса на расстоянии L от вершины конуса? Сделайте схематический рисунок с указанием сил, действующих на шайбу 

С2-27. Полый конус с углом при вершине 2α вращается вокруг вертикальной оси, совпадающей с его осью симметрии. Вершина конуса обращена вверх. На внешней поверхности конуса находится небольшая шайба, коэффициент трения которой о поверхность конуса равен μ. При какой максимальной угловой скорости вращения конуса шайба будет неподвижна относительно конуса, находясь на расстоянии L от вершины? Сделайте рисунок с указанием сил, действующих на шайбу.