С1-1.К колебательному контуру подсоединили источник тока, на клеммах которого напряжение гармонически меняется с частотой ν. Индуктивность L катушки колебательного контура можно плавно менять от максимального значения L_max до минимального L_min, а ёмкость его конденсатора постоянна. Ученик постепенно уменьшал индуктивность катушки от максимального значения до минимального и обнаружил, что амплитуда силы тока в контуре всё время возрастала. Опираясь на свои знания по электродинамике, объясните наблюдения ученика.  

С1-2.К колебательному контуру подсоединили источник тока, на клеммах которого напряжение гармонически меняется с частотой v. Электроёмкость С конденсатора колебательного контура можно плавно менять от минимального значения С_min до максимального С_max, а индуктивность его катушки постоянна. Ученик постепенно увеличивал ёмкость конденсатора от минимального значения до максимального и обнаружил, что амплитуда силы тока в контуре всё время возрастала. Опираясь на свои знания по электродинамике, объясните наблюдения ученика.  

С5-1. Идеальный колебательный контур состоит из конденсатора емкостью 20 мкФ и катушки индуктивностью 8 мГн. Амплитуда колебаний заряда конденсатора 8 нКл. Какова амплитуда колебаний силы тока в контуре?

С5-2. В идеальном колебательном контуре амплитуда колебаний силы тока в катушке индуктивности I_m = 10 мА, а амплитуда напряжения на конденсаторе U_m = 4,0 В. В момент времени t напряжение на конденсаторе равно 3,2 В. Найдите силу тока в катушке в этот момент.

С5-3. В идеальном колебательном контуре амплитуда колебаний силы тока в катушке индуктивности I_m = 5 мА, а амплитуда напряжения на конденсаторе U_m = 2,0 В. В момент времени t напряжение на конденсаторе равно 1,2 В. Найдите силу тока в катушке в этот момент.  

С5-4. В идеальном колебательном контуре происходят свободные электромагнитные колебания. В таблице показано, как изменялся заряд конденсатора в колебательном контуре с течением времени.

С5-5. В идеальном колебательном контуре, состоящем из конденсатора и катушки индуктивности, амплитуда силы тока I_m = 50 мА. В таблице приведены значения разности потенциалов на обкладках конденсатора, измеренные с точностью до 0,1 В в последовательные моменты времени.

Найдите значение электроёмкости конденсатора.  

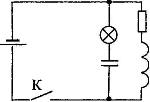С5-7. В электрической цепи, показанной на рисунке, ЭДС источника тока равна 12 В, емкость конденсатора 2 мФ, индуктивность катушки 5 мГн, сопротивление лампы — 5 Ом и сопротивление резистора 3 Ом. В начальный момент времени ключ К замкнут. Какая энергия выделится в лампе после размыкания ключа? Внутренним сопротивлением источника тока пренебречь. Сопротивлением катушки и проводов пренебречь.  

С5-8. Простой колебательный контур содержит конденсатор емкостью С = 1 мкФ и катушку индуктивности L = 0,01 Гн. Какой должна быть емкость конденсатора, чтобы циклическая частота колебаний электрической энергии в контуре увеличилась на Δw = 2×10⁴ с^-1?